Расчет Приведенной (настоящей, текущей) стоимости в EXCEL
Рассчитаем Приведенную (к текущему моменту) стоимость инвестиции при различных способах начисления процента: по формуле простых процентов, сложных процентов, аннуитете и в случае платежей произвольной величины.
Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и Будущей стоимости важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость получается как результат приведения Будущих доходов и расходов к начальному периоду времени и зависит от того, каким методом начисляются проценты: простые проценты , сложные проценты или аннуитет (в файле примера приведено решение задачи для каждого из методов).
Простые проценты
Сущность метода начисления по простым процентам состоит в том, что проценты начисляются в течение всего срока инвестиции на одну и ту же сумму (проценты начисленные за предыдущие периоды, не капитализируются, т.е. на них проценты в последующих периодах не начисляются).
В MS EXCEL для обозначения Приведенной стоимости используется аббревиатура ПС (ПС фигурирует как аргумент в многочисленных финансовых функциях MS EXCEL).
Примечание . В MS EXCEL нет отдельной функции для расчета Приведенной стоимости по методу Простых процентов. Функция ПС() используется для расчета в случае сложных процентов и аннуитета. Хотя, указав в качестве аргумента Кпер значение 1, а в качестве ставки указать i*n, то можно заставить ПС() рассчитать Приведенную стоимость и по методу простых процентов (см. файл примера ).
Для определения Приведенной стоимости при начислении простых процентов воспользуемся формулой для расчета Будущей стоимости (FV): FV = PV * (1+i*n) где PV — Приведенная стоимость (сумма, которая инвестируется в настоящий момент и на которую начисляется процент); i — процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц); n – количество периодов времени, в течение которых начисляются проценты.
Из этой формулы получим, что:
Таким образом, процедура расчета Приведенной стоимости противоположна вычислению Будущей стоимости. Иными словами, с ее помощью мы можем выяснить, какую сумму нам необходимо вложить сегодня для того, чтобы получить определенную сумму в будущем. Например, мы хотим знать, на какую сумму нам сегодня нужно открыть вклад, чтобы накопить через 3 года сумму 100 000р. Пусть в банке действует ставка по вкладам 15% годовых, а процент начисляется только основную сумму вклада (простые проценты). Для того чтобы найти ответ на этот вопрос, нам необходимо рассчитать Приведенную стоимость этой будущей суммы по формуле PV = FV / (1+i*n) = 100000 / (1+0,15*3) = 68 965,52р. Мы получили, что сегодняшняя (текущая, настоящая) сумма 68 965,52р. эквивалентна сумме через 3 года в размере 100 000,00р. (при действующей ставке 15% и начислении по методу простых процентов).
Конечно, метод Приведенной стоимости не учитывает инфляции, рисков банкротства банка и пр. Этот метод эффективно работает для сравнения сумм «при прочих равных условиях». Например, что с помощью него можно ответить на вопрос «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? Чтобы ответить на этот вопрос рассмотрим расчет Приведенной стоимости при начислении сложных процентов.
Сложные проценты
При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».
Приведенную стоимость PV (или ПС) в этом случае можно рассчитать, используя формулу наращения для сложных процентов .
FV = РV*(1+i)^n где FV (или S) – будущая (или наращенная сумма), i — годовая ставка, n — срок ссуды в годах,
При капитализации m раз в год формула Приведенной стоимости выглядит так: PV = FV / (1+i/m)^(n*m) i/m – это ставка за период.
Например, сумма 100 000р. на расчетном счету через 3 года эквивалентна сегодняшней сумме 69 892,49р. при действующей процентной ставке 12% (начисление % ежемесячное; пополнения нет). Результат получен по формуле =100000 / (1+12%/12)^(3*12) или по формуле =ПС(12%/12;3*12;0;-100000).
Отвечая на вопрос из предыдущего раздела «Какое предложение банка выгоднее принять, чтобы получить через 3 года максимальную сумму: открыть вклад с простыми процентами по ставке 15% или со сложными процентами с ежемесячной капитализацией по ставке 12% годовых»? нам нужно сравнить две Приведенные стоимости: 69 892,49р. (сложные проценты) и 68 965,52р. (простые проценты). Т.к. Приведенная стоимость, рассчитанная по предложению банка для вклада с простыми процентами, меньше, то это предложение выгоднее (сегодня нужно вложить денег меньше, чтобы через 3 года получить ту же сумму 100 000,00р.)
Сложные проценты (несколько сумм)
Определим приведенную стоимость нескольких сумм, которые принадлежат разным периодам. Это можно сделать с помощью функции ПС() или альтернативной формулы PV = FV / (1+i)^n
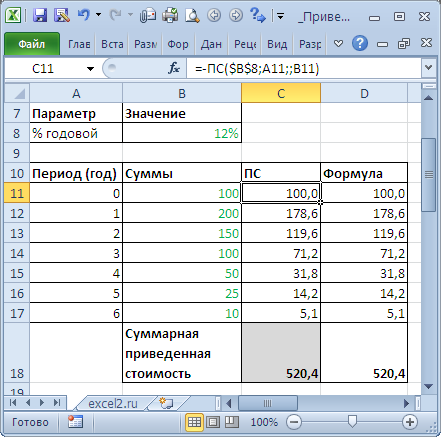
Установив значение ставки дисконтирования равной 0%, получим просто сумму денежных потоков (см. файл примера ).
Аннуитет
Если, помимо начальной инвестиции, через равные периоды времени производятся дополнительные равновеликие платежи (дополнительные инвестиции), то расчет Приведенной стоимости существенно усложняется (см. статью Аннуитет. Определяем в MS EXCEL Приведенную (Текущую) стоимость , где приведен расчет с помощью функции ПС() , а также вывод альтернативной формулы).
Здесь разберем другую задачу (см. файл примера ):
Клиент открыл вклад на срок 1 год под ставку 12% годовых с ежемесячным начислением процентов в конце месяца. Клиент также в конце каждого месяца вносит дополнительные взносы в размере 20000р. Стоимость вклада в конце срока достигла 1000000р. Какова первоначальная сумма вклада?
Решение может быть найдено с помощью функции ПС() : =ПС(12%/12;12;20000;-1000000;0) = 662 347,68р.
Аргумент Ставка указан за период начисления процентов (и, соответственно, дополнительных взносов), т.е. за месяц. Аргумент Кпер – это количество периодов, т.е. 12 (месяцев), т.к. клиент открыл вклад на 1 год. Аргумент Плт — это 20000р., т.е. величина дополнительных взносов. Аргумент Бс — это -1000000р., т.е. будущая стоимость вклада. Знак минус указывает на направление денежных потоков: дополнительные взносы и первоначальная сумма вклада одного знака, т.к. клиент перечисляет эти средства банку, а будущую сумму вклада клиент получит от банка. Это очень важное замечание касается всех функций аннуитета , т.к. в противном случае можно получить некорректный результат. Результат функции ПС() – это первоначальная сумма вклада, она не включает Приведенную стоимость всех дополнительных взносов по 20000р. В этом можно убедиться подсчитав Приведенную стоимость дополнительных взносов. Всего дополнительных взносов было 12, общая сумма 20000р.*12=240000р. Понятно, что при действующей ставке 12% их Приведенная стоимость будет меньше =ПС(12%/12;12;20000) = -225 101,55р. (с точностью до знака). Т.к. эти 12 платежей, сделанные в разные периоды времени, эквивалентны 225 101,55р. на момент открытия вклада, то их можно прибавить к рассчитанной нами первоначальной сумме вклада 662 347,68р. и подсчитать их общую Будущую стоимость = БС(12%/12;12;; 225 101,55+662 347,68) = -1000000,0р., что и требовалось доказать.
Определение Приведенной стоимости в случае платежей произвольной величины
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей (приведенной) стоимости по методу сложных процентов используется функция ЧПС() . Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() . Об этих расчетах читайте в статье Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в MS EXCEL .
]]>
Как рассчитать показатели NPV и IRR в Excel? Финансовый анализ инвестиционного портфеля
В статье будет приведен расчет показателей эффективности проекта, с учетом дисконтирования.
- ЧДД или чистый дисконтированный доход от инвестиционного проекта;
- Внутренняя норма доходности.
Рассмотрим эти два показателя подробнее и рассчитаем пример работы с ними в Excel.
Что такое NPV
Net Present Value (NPV, чистый дисконтированный доход) – один из самых распространенных показателей эффективности инвестиционного проекта.
Это разность между дисконтированными по времени поступлениями от проекта и инвестиционными затратами на него.
Метод расчета NPV:
- Определяем текущую стоимость затрат (инвестиции в проект)
- Производим расчет текущей стоимости денежных поступлений от проекта, для этого доходы за каждый отчетный период приводятся к текущей дате
- CF – денежный поток;
- r – ставка дисконта.
3. Сравниваем текущую стоимость инвестиций (наши затраты) в проект (Io) с текущей стоимостью доходов (PV). Разница между ними будет чистый дисконтированный доход – NPV.
NPV=PV-Io (1)
NPV показывает инвестору доход или убыток от вложений средств в проект по сравнению с доходом от хранения денег в банке.
Если NPV больше 0, то инвестиции принесут больше дохода, нежели чем аналогичный вклад в банке.
Формула 1 модифицируется если инвестиционные вложения в проект осуществляются в несколько этапов (периодов).
CF – денежный поток;
I — сумма инвестиционных вложений в проект в t-ом периоде;
r — ставка дисконтирования;
n — количество периодов.
Internal Rate of Return (Внутренняя норма доходности, IRR) определяет ставку дисконтирования при которой инвестиции равны 0 (NPV=0), или другими словами затраты на проект равны его доходам.
IRR = r, при которой NPV = f(r) = 0, находим из формулы:
- CF – денежный поток;
- I — сумма инвестиционных вложений в проект в t-ом периоде;
- n — количество периодов.
Этот показатель показывает норму доходности или возможные затраты при вложении денежных средств в проект (в процентах).
Пример расчета NPV в Excel
В MS Excel 2010 для расчета NPV используется функция =ЧПС().
Найдем чистый дисконтированный доход (NPV) проекта, требующего вложений инвестиций на 90 тыс. руб., и денежный поток которого распределен по времени рис 1. , и ставка дисконта равна 10%.
Рассчитаем показатель NPV по формуле Excel:
=ЧПС(D3;C3;C4:C11)
D3 – ставка дисконта;
C3 – вложения в 0 периоде (наши инвестиционные затраты в проект);
C4:C11 – денежный поток проекта за 8 периодов.
В итоге показатель чистого дисконтированного дохода равен 51,07 >0, это говорит о том, что в проект стоит инвестировать.
Расчет IRR в Excel
Для определения IRR в Excel используется встроенная функция
=ЧИСТВНДОХ()
Но так как у нас в примере данные поступали в равные интервалы времени можно использовать функцию =ВСД(C3:C11)
Доходность вложения в проект равна 38%.
В завершение картинка финансового анализа проекта целиком.
Узнай о других возможностях Excel на курсе «Excel Academy» от SF Education!
]]>Расчет NPV
Понятие NPV
NPV (Net Present Value, ЧДД, чистый дисконтированный доход, чистая приведенная стоимость, чистый приведенный доход) — это такой показатель эффективности инвестиционного проекта, который позволяет суммарно оценить платежи при реализации инвестиционного проекта, приведенные к настоящему моменту времени. Как правило, если значение NPV > 0, то инвестиционный проект считается эффективным, если NPV
Формула расчета NPV
Расчет NPV в общем случае осуществляется по следующей формуле:
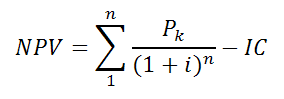Формула расчета NPV
где Рк — величины денежных поступлений в течении n лет;
IC — величина первоначальных инвестиций;
i — ставка дисконтирования.
Возможны варианты, когда реализация инвестиционного проекта связана не с разовыми первоначальными инвестициями, а предполагает инвестирование в течении нескольких периодов. Тогда расчет NPV осуществляется по следующей формуле:
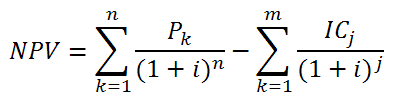Формула расчета NPV при инвестировании в течении нескольких периодов
Пример расчета NPV
Приведем пример расчета NPV условного инвестиционного проекта. Предположим, что объем инвестиций в новое здание составляет 15000 тыс.руб.; прогноз ежегодного дохода от сдачи помещений в аренду составляет 5000 тыс.руб. в течении 5-ти лет. Ставка дисконтирования составляет 17%. Рассчитать NPV.
Расчет NPV: NPV = 5000/1.17 + 5000/1.17 2 + 5000/1.17 3 + 5000/1.17 4 + 5000/1.17 5 — 15000 = 15996.73 — 15000 = 996.73 тыс.руб.
Так как рассчитанная величина NPV > 0, то проект может быть принят к практической реализации.
Как уже указывалось ранее, условия инвестирования при реализации проекта могут быть различные. Рассмотрим пример вычисления чистого приведенного эффекта (дохода) в случае, когда вложение средств осуществляется единовременно, а годовые поступления от реализации инвестиционного проекта не равны между собой. Предположим, что объем инвестиций составил 12500 тыс.руб., срок реализации проекта — 5 лет, цена вложенных средств составляет 12,5% годовых, поступления по годам от реализации инвестиционного проекта следующие (в тыс.руб.): 2500; 2250; 1980; 1850; 1720. Определим величину чистого приведенного эффекта: ЧДД = 2500*1,125 -1 + 2250*1,125 -2 + 1980*1,125 -3 + 1850*1,125 -4 + 1720*1,125 -5 — 12500 = -4999,96. Так как значение рассматриваемого показателя меньше 0, то рассматриваемый условный проект не будет приносить прибыли при своем осуществлении и должен быть отвергнут.
Рассмотрим также пример расчета дисконтированного чистого дохода в случае, когда доходы от вложенных средств начинают поступать уже после завершения инвестиционного проекта, т.е. денежный поток включает в себя не только положительные, но и отрицательные величины. Например, имеется инвестиционный проект со следующими показателями потоков платежей (в тыс.руб.): -215; -295; 50; 500; 300; 800; 1000. Цена инвестированного капитала составляет 14% годовых. Вычислим значение чистого приведенного эффекта (дохода): ЧДД = (-215)*1,14 -1 + (-295) *1,14 -2 + 50*1,14 -3 + 500*1,14 -4 + 300*1,14 -5 + 800*1,14 -6 + 1000*1,14 -7 = 834,12. Величина ЧДД положительна, следовательно, проект может быть принят к практическому осуществлению.
Рассмотрим пример расчета NPV в Excel. Первым шагом вычисления рассматриваемого показателя будет подготовка исходных данных в Excel. Широкий спектр возможностей указанного табличного процессора позволяет исходные данные представить во множестве вариантов (в том числе и с различным оформлением и форматированием), один из которых приведен на рисунке:
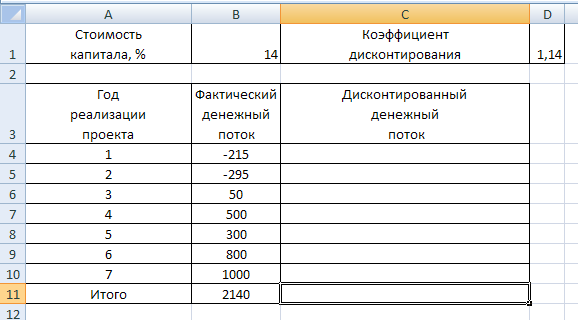Исходные данные для расчета NPV в Excel
Далее для вычисления чистого приведенного эффекта (дохода) в ячейки C4:C11 необходимо ввести формулы, по котором будет вычислен ЧДД для каждого года реализации проекта. Сделать это можно следующим образом: