Как определять доходность инвестиции

Как не ошибиться, рассчитывая среднюю доходность инвестиций, что такое «подножка волатильности», и почему умелая диверсификация не только обеспечивает стабильность инвестиционного портфеля, но и улучшает доходность.

Все инвесторы сталкиваются с необходимостью расчета средней доходности своего портфеля. Это нужно для того чтобы прогнозировать его будущую стоимость. Без такого прогноза невозможно, например, решить, на какую сумму следует пополнять инвестиционный портфель, чтобы достичь поставленных целей к сроку.

Часто инвесторы ошибаются в расчетах, потому что используют неправильную формулу. Использовать ошибочную оценку в планировании будущих действий опасно. Ценой просчета может стать качество жизни в старости или образование ребенка.

Как правильно оценить среднюю доходность

Среднюю доходность портфеля в заданном периоде нужно считать не как среднюю арифметическую, а как среднюю геометрическую. Разберемся на простом примере.

Допустим инвестор вкладывает деньги в российские акции через фонд А и российские облиции через фонд Б в пропорциях 60 на 40. Ниже в таблице приведены данные по ежегодной динамике стоимости акций, облигаций и совокупного портфеля.

Таблица №1. Доходности фондов А, Б и портфеля 60/40 за 4 года (в руб).

Инструмент	2016	2017	2018	2019
Фонд А	28,67%	-2,22%	16,74%	37,44%
Фонд Б	15,24%	14,83%	2,7%	15,34%
Портфель 60/40	23,30%	4,60%	11,12%	28,60%

Акции, облигации и портфель за все время принесли 101,86%, 56,74% и 83,81%. На первый взгляд получается 20,16%, 12% и 16,9% в среднем за год. На самом же деле эти цифры завышены. Как так вышло? Дело в том, что арифметическая средняя (сумма доходностей, поделенная на количество периодов) не походит для расчета инвестиционных результатов, так как доходность, полученная в очередном периоде, относится к стоимости портфеля в предыдущем периоде, и включает доходность на доходность прошлого периода, а не только на сумму инвестиций. Например, если портфель упал на 5% за период с уровня 10000, а затем поднялся на 5%, он не вернется к 10000, а будет стоить 9975 руб. В этом примере разница небольшая, но чем больше рыночная нестабильность, то тем больше будет расхождение. — это прекрасно видно на примере фонда А, который является более волатильным, чем фонд Б.

Для того, чтобы правильно учесть волатильность доходностей и их влияние на результат используют среднюю геометрическую или, как еще её называют, аннуализированную доходность (Compound Average Growth Rate). Она рассчитывается как корень степени n из произведения доходностей за n периодов. Например, ∜(1,232 * 1,046 * 1,1112 * 1,286) даст среднюю доходность портфеля в 16,5% в год (а не 16,7%, как средняя арифметическая). Как и средняя арифметическая, средняя геометрическая не всегда соответствует показателю в каждый конкретный год, но при этом в конце периода она трансформирует первоначально инвестированную сумму в точный итоговый результат инвестирования. Как следствие, именно этот показатель, а не среднюю арифметическую доходность стоит использовать для долгосрочного инвестиционного планирования. Сравнение динамики средней арифметической и реальной доходностей представлены в таблице №2 и на графике №1.

График №1. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Таблица №2. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Источник: Bloomberg, расчеты FinEx

Что такое подножка волатильности?

Разницу между средней арифметической и средней геометрической доходностью в академических кругах называют «volatility drag» или «подножка волатильности». Почему же речь идет о «подножке»? Потому что с точки зрения математики, чем более волатилен ряд доходностей, тем сильнее геометрическая доходность будет отставать от арифметической.

Volatility Drag = средняя арифметическая доходность — средняя геометрическая доходность

Несмотря на свою простоту, это формула позволяет сделать ряд интересных выводов — например, относительно опасности популярных у многих инвесторов инвестиций с использованием заемных средств («финансового рычага»). Когда инвестор рискует не только собственными средствами, но и занимает дополнительные деньги у своего брокера для того, чтобы увеличить размер своего портфеля, он увеличивает и его волатильность.

Например, использование рычага 2 (на каждый вложенный собственный рубль инвестиций инвестор получает в кредит еще один рубль и инвестирует его в рынок) обеспечивает удвоение арифметической доходности (без учета расходов в связи с использованием рычага). Но в случае падения, удваиваются и потери. В результате из-за бремени волатильности средняя геометрическая доходность меняется медленнее.

Как диверсификация отражается на волатильности портфеля?

Диверсификация портфеля сокращает volatility drag и поэтому положительно сказывается на доходности портфеля. Рассмотрим простой пример: инвестор может инвестировать в акции компании А или в акции компании А и Б. Волатильность акций компании А 26%, Б – 11%, их годовые доходности и результаты инвестирования для первого и второго случая представлены в таблице ниже. Как видно из таблицы, из-за большей волатильности первого инструмента, даже большие номинальные доходности несут в итоге результат хуже, чем в случае с инвестированием в разные инструменты даже пусть с меньшей общей доходностью. Это происходит как раз из-за того, что волатильность съедает большую доходность. Во втором случае портфель падает меньше чем при инвестировании исключительно в акции А, и даже небольшая доходность дает лучший итоговый результат в 6,7% за 10 лет.

График №2. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Источник: Bloomberg, расчеты FinEx

Таблица №3. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Как измерить эффективность инвестиционного портфеля: 3 практических подхода

Многие начинающие инвесторы оценивают эффективность собранного ими портфеля активов исключительно на основе полученной прибыли. Это не совсем верно, ведь такой подход совсем не учитывает риск, который сопутствовал получению дохода.

Сегодня мы поговорим о нескольких подходах к оценке результативности инвестиционного портфеля.

Коэффициент Трейнора

Это составная мера эффективности портфеля, которая включает и риск. При этом автор формулы предположил, что существует два компонента риска: риск, порожденный флуктуациями на рынке, и риск, который возникает вследствие колебаний конкретного актива.

Коэффициент Трейнора еще называют коэффициентом вознаграждения к волатильности – он является показателем доходности, которая превышает доходность, которая могла бы быть получена по безрисковым инвестициям, на каждую единицу рынка. Важный момент: при расчете коэффициента доходность соотносится только с систематическим риском, а не с общим.

То есть, чем выше коэффициент Трейнора, тем более эффективен инвестиционный портфель. Рассчитывается этот коэффициент так:

r_i=доходность портфеля
r_f=безрисковая процентная ставка
β=бета (коэффициент риска)
​
Портал Investopedia приводит пример использования коэффициента Трейнора в реальных инвестициях. Можно предположить, что десятилетняя доходность индекса S&P 500 (рыночный портфель) составляет 10% годовых, а средний годовой доход от казначейских бондов США (как замена безрисковой процентной ставки) составляет 5%. Также, предположим, что есть три управляющих портфелями, которые показали следующие 10-летние результаты

Управляющие	Средняя годовая доходность	Бета
А	10%	0,90
B	14%	1,03
C	15%	1,20

Коэффициент Трейнора для каждого из них будет таким:

Вычисление	Коэффициент Трейнора
T(market)	(0.10-0.05)/1	0,05
T(manager A)	(0.10-0.05)/0.90	0,056
T(manager B)	(0.14-0.05)/1.03	0,087
T(manager C)	(0.15-0.05)/1.20	0,083

Чем выше коэффициент, тем эффективнее портфель. Таким образом, если основываться только на доходности, то менеджер B кажется наиболее результативным. Но если оценивать связанные с его деятельностью риски, то окажется, что на самом деле лучший результат показал управляющий B.

Коэффициент Шарпа

Эта мера очень похожа на коэффициент Трейнора, но здесь риск – это стандартное отклонение портфеля, а не систематический риск, представленный бетой.

Формула для расчета коэффициента Шарпа выглядит так:

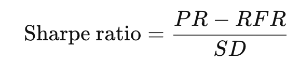
PR=доходность портфеля
RFR=безрисковая процентная ставка
SD=стандартное отклонение
​
Используя пример из предыдущего раздела, у индекса S&P 500 стандартное отклонение находится на уровне 18% за десятилетний период. Тогда для управляющих портфелями коэффициент Шарпа будет выглядеть так:

Управляющий	Годовая доходность	Стандартное отклонение портфеля
X	14%	0,11
Y	17%	0,20
Z	19%	0,27

S(market)	(0.10-0.05)/0.18	0,278
S(managerX	(0.14-0.05)/0.11	0,818
S(manager Y)	(0.17-0.05)/0.20	0,600
S(manager Z)	(0.19-0.05)/0.27	0,519

Как и в предыдущем случае, оказывается, что лучший портфель не обязательно тот, что приносит наибольшее количество денег. Напротив, наилучший результат – это доходность в совокупности с приемлемым риском.

В отличие от коэффициента Трейнора, коэффициент Шарпа оценивает результативность с учетом диверсификации. Таким образом, эта мера лучше подходит для оценки хорошо диверсифицированных инвестпортфелей.

Коэффициент Йенсена

Эта мера рассчитывается с помощью модели CAPM (Capital Asset Pricing Model), по-русски ее еще называют моделью оценки долгосрочных активов. Ее суть в том, что величина требуемой доходности на вложенные средства определяется не столько специфическим риском актива, а общим уровнем риска всего рынка в целом.

Коэффициент Йенсена в итоге подсчитывает избыточную доходность, которую портфель приносит с превышением ожидаемой доходности. Эта мера доходности называется альфой.

Говоря проще, коффициент Йенсена измеряет, насколько доходность портфеля связана со способностью управляющего портфелем генерировать результаты выше среднего по рынку, с учетом риска. Чем выше коэффициент, тем лучше доходность с учетом риска. Портфолио с последовательно положительным превышающим ожидания доходом будет иметь положительную альфу, и наоборот.

Формула расчета выглядит так: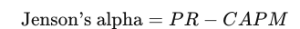
,

PR=доходность портфеля
CAPM=безрисковая процентная ставка + β(доходность рыночной безрисковой процентной ставки)

Если предположить, что безрисковая процентная ставка находится на уровне 5% и рыночная доходность на уровне 10%, какова будет альфа следующих портфелей?

Управляющий	Годовая доходность	Бета
D	11%	0,90
E	15%	1,10
F	15%	1,20

ER(D	0,05 + 0,90 (0,10-0,05)	0,0950 или 9,5% доходности
ER(E)	0,05 + 1,10 (0,10-0,05)	0,1050 или 10,5% доходности
ER(F)	0,05 + 1,20 (0,10-0,05)	0,1100 или 11% доходности

Подсчет альфы происходит посредством вычитания ожидаемого дохода из реальной доходности:

Alpha D	11%- 9,5%	1,5%
Alpha E	15%- 10,5%	4,5%
Alpha F	15%- 11%	4,0%

Какой же портфель и его управляющий показал лучшие результаты? Управляющий Е оказался лучше всех, поскольку, хоть менеджер F показал такой же уровень доходности, ожидаемая доходность в случае Е была ниже, а бета портфеля была значительно ниже, чем в случае портфеля F.

Важный момент: оценка доходности и риска для акций и портфелей будет меняться со временем. Коэффициент Йенсена требует использование различных безрисковых ставок для каждого интервала. То есть для оценки производительности на пятилетнем отрезке с использованием годовых интервалов, потребуется еще и изучить годовую доходность за вычетом безрискового дохода для каждого года и соотнести ее с годовой доходностью рыночного портфеля минус та же безрисковая ставка.

Источник https://finex-etf.ru/university/news/kak_schitat_dokhodnost_investitsiy/

Источник https://habr.com/ru/company/iticapital/blog/489902/

Источник

Источник